Search Strategies

In AI problems, it is important to use search strategies to find the goal in them.

Search Types

• Uniformed Search (Blind Search) 盲目搜索
  No other information like path cost or the number of steps are given. Only could it do is to distinguish from goal state from non-goal state.

  • Types
    • Breadth-first Search
    • Uniform-cost Search
    • Depth-first Search
    • Depth-limited Search
    • Iterative Deeping Search
    • Bidirectional Search

• Informed Search (Heuristic Search) 启发式搜索
  　Giving some other information to help finding the goal state.

Performance Measurement

• Completeness 完成性
  Whether the algorithm guarantee to find the solution if there is any.

• Optimality 最优性
  Whether the algorithm could find the optimal solution.

• Time Complexity 时间复杂度
  Time cost of the algorithm.

• Space Complexity 空间复杂度
  Memory cost of the algorithm.

O-natation

$O(g(n))={f(n): \text{there exist positive constants } c \text{ and } n_0 \text{ such that for all } n>=n_0}$

*i.e. When $n>=n_0, f(n)<=cg(n).$
$g(n)$ is an asymptotic upper bound (渐进上界) for $f(n)$. If $f(n) \in O(g(n))$, we write $f(n)=O(g(n))$.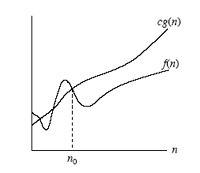

*$g(n)$ is a set of functions.
*O stand for the order of growth of $f(n)$. O 的含义是 $f(n)$ 的数量级，$g(n)$ 是算法中基本运算的频度。

Breadth-first Search

• Search every node in the certain level before going to next level.

• Branching Factor: The maximum number of children for each internal node in a tree.

• Suppose the branching factor is 2. When the solution node is at the level $d+1$, it should expand the maximum number of node to be $1+2+2^2+2^3+...+2^d=2^{d+1}-1=O(2^d)$.

• Advantages

  • Complete (It is guarantee to find solution if there is any)
  • Always find the shallowest goal first when there are multi-solutions.

• Drawback

  • Memory and time cost may not support due to it must maintained all the nodes in memory at the same time.

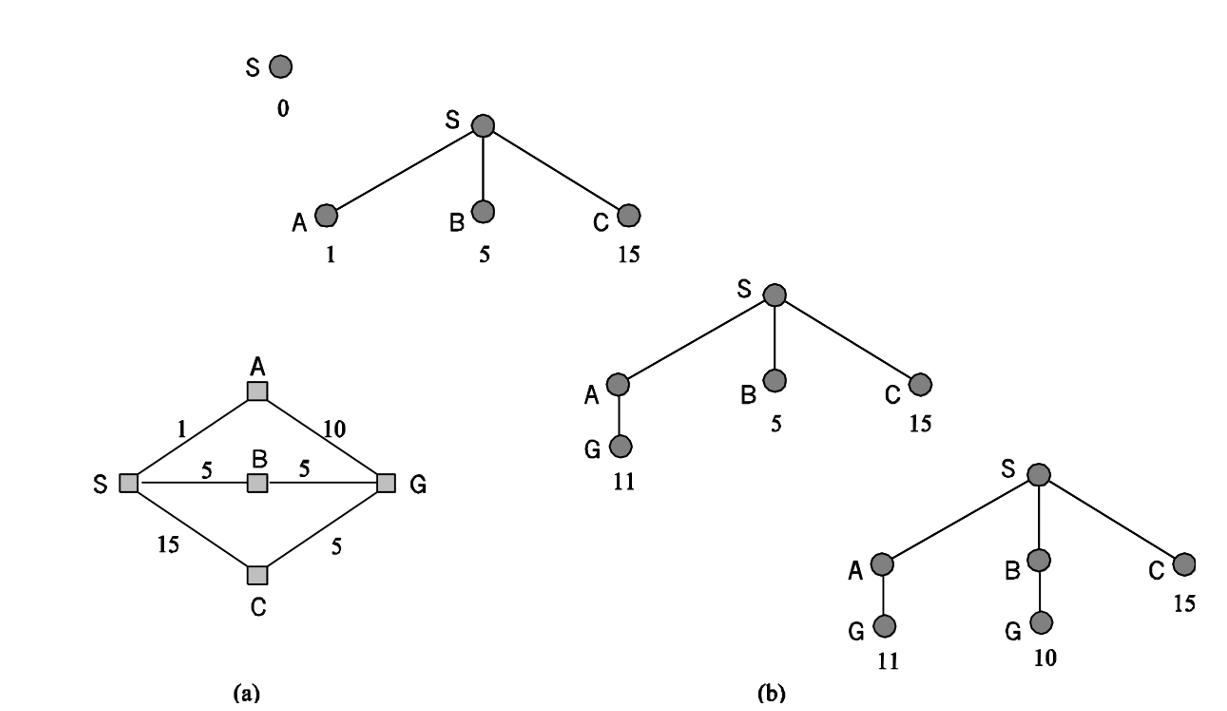
Uniform Cost Search

• Modifies the Bread-first search strategy by always expanding the lowest-cost node.
• The first solution found is guaranteed to be the cheapest solution.
  

Depth-first Search

• Depth-first search always expands the node at the deepest level of the tree.
  

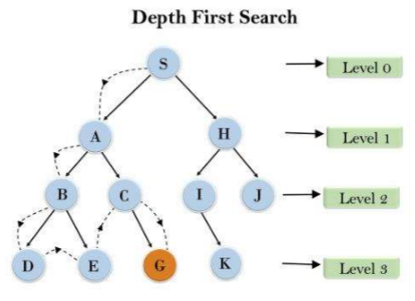
• Advantages

  • Have modest memory Requirement. Only store a single path from the root to a leaf node, along with the remaining unexpanded sibling nodes for each node on the path. For branch factor $b$ and maximum depth $m$, it only need $bm$ nodes to storage.
  • Time complexity is $O(b^m)$.

• Drawbacks

  • May stuck when going down the wrong path (infinite loop).
  • May find a solution path longer than optimal solution.
  • Neither complete nor optimal.

References

[1] Y.M. Cheung. COMP 7015 Artificial Intelligence. Hong Kong Baptist University, 2020
[2] 王道论坛.2020 年数据结构考研复习指导[M].北京:电子工业出版社, 2019