Logistic Regression as a Neural Network
Notation
$(x,y)$
A single training example. Where $x\in{\mathbb{R}^{n_x}}$ ($x$ is a x-dimensional feature vector), $y\in {(0, 1)}$.$m:{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})}$ or $m={ m_{train}}$
A training set which contains m training examples.$m={m_{test}}$
A test example set.$X=[x^{(1)}, x^{(2)}, ..., x^{(m)}]$
Input training example matrix which has $n_x$ rows and $m$ columns. $X\in{\mathbb{R}^{n_x * m}}$.WARNING
It is not a good idea to put training examples $x^{(1)\mathrm{T}}, ..., x^{(m)\mathrm{T}}$ as row vectors in the matrix $X$. It will cause much more efforts when computing.
$Y=[y^{(1)}, y^{(2)}, ..., y^{(m)}]$
Output matrix which has $1$ row and $m$ columns. $Y\in{\mathbb{R}^{1 * m}}$.
Binary Classification
Logistic regression is an algorithm for binary classification (Used for the supervised learning problem which the output labels $y$ are all either 0 or 1).
Scenario example
Take a picture as an input, and want to get a label for output to infer whether the picture is a cat. Define the output label $y$ is 1 as the picture is the case of a cat picture, and the output label is 0 as the picture is the case of not a cat picture.
To Be Specific
Say, the picture is 64 × 64 pixels. And it can be divided as 3 matrices representing the red, green and blue channel.
Define the feature vector $x$ as the every elements unroll by the color matrices. So, the dimension of the feature vector $x$ is 12288. Marked as:
$$n=n_x=12288$$
Goal: Classifier $x->y$ can predict whether the label $y$ is 1 or 0.
Logistic Regression
Example
Given a feature vector $x$ and wanting to know the probability $\hat{y}$ of output label $y = 1$ (i.e. $\hat{y}=P(y=1|x)$).
Parameters
$w\in{\mathbb{R}^{n_x}}, b\in{\mathbb{R}}$
*$w$ stand for weight, which could tell the algorithm where to focus on. $b$ stand for bias, which could make sure that the neuron will be activate meaningfully (i.e. How high the weighted sum needs to be before the neuron starts getting meaningfully active.).
Output
$\hat{y}=w^\mathrm{T}x+b$ (Linear Regression. Will not be worked, $\hat{y}$ is not between 0 and 1.)
$\hat{y}=\sigma(w^\mathrm{T}x+b)$ (Sigmoid Function, i.e. $\sigma(z)=\frac{1}{1+e^{-z}}$)
About Sigmoid Function
The graph of sigmoid function
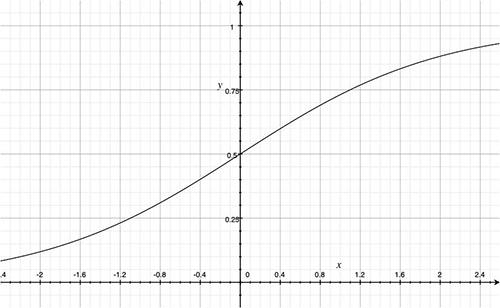
Features
$\lim \limits_{z \to +\infty} \sigma(z) = 1$
$\lim \limits_{z \to -\infty} \sigma(z) = 0$
Logistic Regression Cost Function
Using a cost function to train the parameters $w$ and $b$ of the logistic regression model.
Loss (Error) Function
A function used to measure how well the algorithm is doing. (For single training example)
Square Error
$$\mathcal{L}(\hat{y}, y) =\frac{(\hat{y}-y)^{2}}{2}$$
Not usually use. The optimization problem always becomes non-convex. Therefore, there will be more than one multiple local optima. It can not using for gradient descent to find the global optimum.Cross-Entropy Loss Function
$$\mathcal{L}(\hat{y}, y) =-[y \log (\hat{y})+(1-y) \log (1-\hat{y})]$$
The lower value of loss function is, the better prediction of algorithm is.[Analyse]
- If $y=1$, $\mathcal{L}(\hat{y}, y)=-\log (\hat{y})$.
When $\mathcal{L}$ is small, $\log (\hat{y})$ should be large, and $\hat{y}$ should be large as well but no more than $1$. - If $y=0$, $\mathcal{L}(\hat{y}, y)=-\log (1-\hat{y})$.
When $\mathcal{L}$ is small, $log (1-\hat{y})$ should be large, and $\hat{y}$ should be small but no less than $0$.
- If $y=1$, $\mathcal{L}(\hat{y}, y)=-\log (\hat{y})$.
Cost Function
A function used to measure how well the algorithm is doing. (For the whole training set)
$$J(w, b)=\frac{1}{m} \sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)})=-\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log (\hat{y}^{(i)})+(1-y^{(i)}) \log (1-\hat{y}^{(i)})]$$
Still, the lower value of cost function is, the better prediction of algorithm is.
Gradient Descent
A algorithm to train (learn) the parameters $w$ and $b$ on the training set. Take all the $w$ and $b$ as the parameters, the gradient descent algorithm will find out the global optimum which is the point can having the smallest value of cost function. In another word, gradient descent tells what nudges to all of the weights and biases cause the fastest change to the value of the cost function. (i.e. Which changes to weights matter the most.)
[Analyse]
Only analyse the value $J(w)$ and parameter $w$. Assume that the funtion $J(w)$ is a convex function. Repeat this algorithm until the algorithm converges.
*$\alpha$ is the learning rate. It controls how big a strep the algorithm take on each iteration.
*When writing code, $\frac{d J(w)}{d w}$ will be defined as dw.
And for the real cost function, the gradient descent will be like:
*When writing code, $\frac{\partial J(w, b)}{\partial w}$ will be defined as dw, and $\frac{\partial J(w, b)}{\partial b}$ will be defined as db.
*Also, a coding convention dvar represent the derivative of a final output variable with respect to various intermediate quantities
Logistic Regression Gradient Descent
[Analyse]
For a training example which has two features.
$z=w^\mathrm{T}x+b$
$\hat{y}=a=\sigma(z)$
$\mathcal{L}(a, y)=-[y \log (\hat{y})+(1-y) \log (1-\hat{y})]$
features: $x_1$ and $x_2$
parameters: $w_1$, $w_2$ and $b$
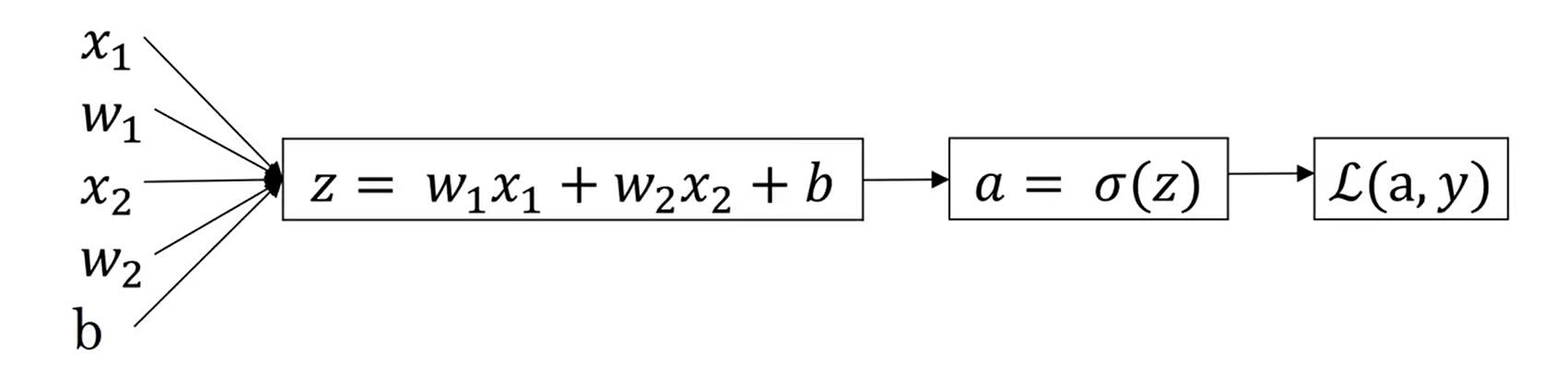
da:
$$ \frac{\partial \mathcal{L}(a, y)}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}$$
dz:
dw1:
$$ \frac{\partial \mathcal{L}(a, y)}{\partial w_{1}}=x_{1} \cdot d z$$
dw2:
$$ \frac{\partial \mathcal{L}(a, y)}{\partial w_{2}}=x_{2} \cdot d z$$
db:
$$ \frac{\partial \mathcal{L}(a, y)}{\partial b}=d z$$
Gradient Descent on m Examples Training Set
[Analyse]
For a m training examples training set, and each training example have two features.
$z=w^\mathrm{T}x^{(i)}+b$
$\hat{y}^{(i)}=a^{(i)}=\sigma(z)$
$J(w,b)=\frac{1}{m} \sum_{i=1}^{m}L(a^{(i)}, y^{(i)})$
features: $x_1^{(i)}$ and $x_2^{(i)}$
parameters: $w_1$, $w_2$ and $b$
Overall training set gradient descent with the respect of $w_1$:
$$ \frac{\partial J(w, b)}{\partial w_{1}}=\frac{1}{m} \sum_{i=1}^{m} \frac{\partial \mathcal{L}(a, y)}{\partial w_{1}}$$
For single training example $(x^{(i)},y^{(i)})$, use the algorithm showed before. Then add up and divided by m to get the overall result:
// Initialize
J = 0;
dw1 = 0; // as a accumulator for whole training set
dw2 = 0; // as a accumulator for whole training set
db = 0; // as a accumulator for whole training set
// Add up
for(i = 1 to m) {
z(i) = wT x(i) + b;
a(i) = σ(z(i));
J += -[y(i) log(a(i)) + (1 - y(i)) log(1 - a(i))];
dz(i) = a(i) - y(i);
dw1 += x1(i) dz(i);
dw2 += x2(i) dz(i);
db += dz(i);
}
// Get average
J /= m;
dw1 /= m; // geting the value of dJ/dw1
dw2 /= m; // geting the value of dJ/dw2
db /= m; // geting the value of dJ/dbTIP
In the algorithm, there are two for-loop nested (The second for-loop used for calculate every $w$s and $b$s with the respect to every features). When having a large scale training set it will run less efficiency. Using vectorization to solve this problem.